Chemistry 2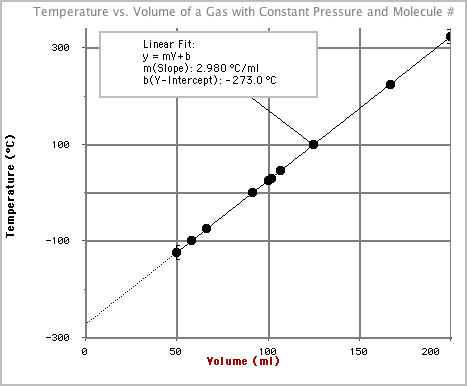

Charles' Law

  1. Below is the data table you used to relate temperature and volume:
    Trial
    T (°C)
    V (mL)
    1

    -124.00
    50.00
    2
    -100.00
    58.05
    3
    -75.00
    66.44
    4
    0.00
    91.61
    5
    25.00
    100.00
    6
    30.00
    101.68
    7
    45.00
    106.71
    8
    100.00
    125.17
    9
    225.00
    167.11
    10
    323.00
    200.00
  2. Notice that as we make a gas colder its volume decreases. This makes sense with our understanding of Kinetic Molecular Theory. If the molecules of a gas were considered to be point particles with no size then at some cold temperature, as the molecules slowed more and more, we could shrink the volume of a gas to zero. At this point we have reached the smallest possible volume, which implies that we have also reached the lowest possible temperature. This is known as absolute zero.
  3. By looking at the graph above and the best fit line for the data collected we can see that this occurs at -273°C. Wouldn't it make sense that if there is a coldest possible temperature that we should start the temperature scale at 0 instead of -273? Lord Kelvin believed this, so he devised a temperature scale that was equivalent in every way to the Celsius scale, except it started at 0 instead of -273. This is called the Kelvin temperature scale. Click on the image to see a comparison of the various temperature scales.
  4. So to convert Celsius to Kelvin just add 273. To convert Kelvin to Celsius subtract 273. (The conversion between F and Celsius is a bit more complicated C = 5*(F-32)/9 ).
  5. Lets redo our graph using the Kelvin temperature scale:
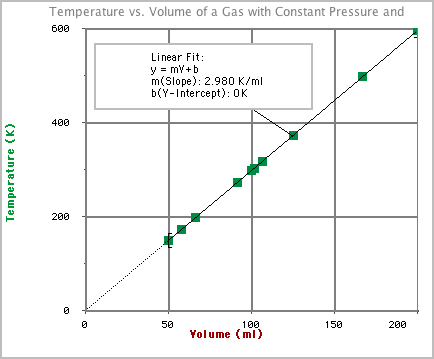
  6. Notice that the function for the best fit line is now simplified. If the Y intercept (b) is zero then the function becomes: y = m*V.
  7. Let's see if we can derive some simple relationship between Temperature and Volume:
    y = constant*x or
    T = constant*V or
    T/V = constant or
    V/T = 1/constant = constant2 so
    V1/T1 = V2/T2
  8. Here we see Charles' Law appear before our eyes:
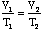
  9. If we don't use the Kelvin temperature scale then the equation would be:
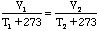
  10. So, whenever we do calculations with gasses we must use the Kelvin temperature scale and the simple version of Charles' Law.
  11. Two assumptions about the experimental conditions must be made for this relationship to be true. What are they? (What other factors can affect temperature or volume?)
  12. Look back at Kelvin temperature graph. Notice that as the Kelvin temperature doubles, the volume also doubles. When the volume was decreased by half, this occurred because the Kelvin temperature was cut in half. This kind of relationship is known as directly proportional and will give you a graph shaped like the one above.
  13. Let's do an example problem: Let's say you are outside on a cold winter day when the temperature is -5.00°C and you inflate a balloon to a volume of 500.0 mL. Then you take your balloon into a sauna where the temperature is 43.0°C. What would be the new volume of the balloon? Click here to see the answer.