Chemistry 2

Combined Gas Law

  1. To use Boyle's Law we have to make sure the temperature and number of moles stays constant.
  2. To use Charles' Law we have to make sure the pressure and number of moles stays constant.
  3. To keep the moles constant is relatively easy, because we just have to make sure there are no leaks in the gas container. Keeping temperature or pressure constant is more difficult because they influence each other.
  4. To overcome this we can do two sets of calculation, one using Boyle's Law, and then one using Charles' Law. Here is the example from the front side of the Combined Gas Law Sheet.

    "You blow a methane bubble with a volume of 200.0mL at a pressure of 1.00 atm and a temperature of 20.0°C. Because methane is lighter than air, the bubble floats upward until it reaches and an altitude where the pressure is 0.600 atm and a temperature of -10.0°C."

    1. Using Boyle's Law we can calculate the new volume of the bubble just due to the pressure change:
      Sea Level High Altitude
      P1 = 1.00 atm P2 = 0.600 atm
      V1 = 200.0 ml V2 = ?




    2. Using Charles' Law we can take this new larger bubble due to the pressure change and let it cool down due to the temperature change:
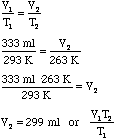
      Warm High Altitude
      		Cool High Altitude
      T1 = 20.0°C = 293 K T2 = -10.0°C = 263 K
      V1 = 333 ml V2 = ?





    3. Notice that the V2 from the first problem was substituted for the V1 in the second problem. We can substitute this algebraically as follows:

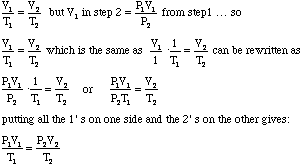
    4. Voila we have the Combined Gas Law! This can be used to solve any of the problems we have encountered so far, even those in which pressure, volume, or temperature do remain constant. In problems such as these the constant property will mathematically cancel out on each side.
    5. Solving the above problem using the Combined Gas Law is as follows:
      Warm Sea Level Cool High Altitude
      P1 = 1.00 atm P2 = 0.600 atm

      V1 = 200.0 mL

      		 V2 = ?

      T1 = 293 K

      		 T2 = 263 K