Chemistry 2

Significant Digits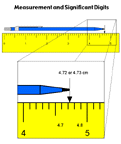

  1. All measurements have some limit to their precision. You can only be as precise as the instrument used to make the measurement.
  2. The digits which are considered significant are all the measured digits plus one estimated digit. How many significant digits were there in each of the measurements I made with the various rulers during the demonstration?
  3. Here are some rules to help determine how many significant digits are in a number
  4. In the last example, where the number 19000 has an ambiguous number of significant digits, scientific notation will clear up this problem. 11000 can be written several ways in scientific notation to indicate a certain amount of significant digits.
    1.90 x 104
    =
    		19000 and has 3 significant digits.
    1.9 x 104
    =
    		19000 and has 2 significant digits.
    1.9000 x 104
    =
    		19000 and has 5 significant digits.
  5. Try counting the significant digits in following set of numbers
    3.456
    5.000
    10003
    0.666
    5.001
    0.00300
    5
    0.005
    314.000
    10000
    12000
    10000.0
    100321
    90210
    314000
    see answers below

    For more significant digit practice use a Flash based significant figure problem generator.
  6. Significant digits in calculations
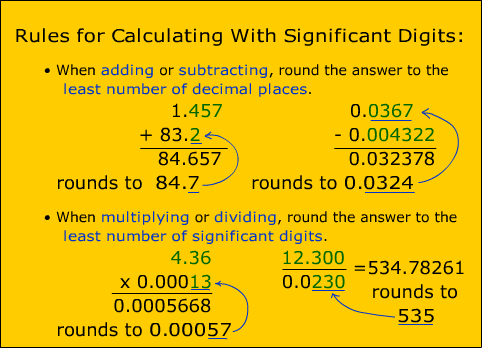
    2. Addition and subtraction example:
      1. Let's say two measurements were taken and they came out to 1.3 cm and 2.54 cm. The last digit of these measurements was estimated so 1.3 cm could be anything from 1.2 - 1.4 cm (or even broader), and 2.54 cm could be anything from 2.53 - 2.55 cm (or even broader). Let's assume we will need to add these measurements together for a calculation.
      2. The lowest possible right answer is: 1.2 cm + 2.53 cm = 3.73 cm
        The highest possible right answer is: 1.4 cm + 2.55 cm = 3.95 cm
      3. Notice that the tenths place varies, so it doesn't make any sense to pretend we have any information about the hundredths place and should not report it. We should round this answer to the tenths place.
      4. Using our original measurements we get: 1.3 cm + 2.54 cm = 3.84 cm --- rounded to ---> 3.8 cm
    3. Multiplication and division example:
      1. Let's assume we have the same two new measurements: 12 cm (implied range of 11 - 13 cm) and 1.33 cm (implied range of 1.32 - 1.34 cm). What if we needed to multiply them together to solve a problem.
      2. The lowest possible right answer is: 11 cm x 1.32 cm = 14.52 cm2
        The highest possible right answer is: 13 cm x 1.34cm = 17.42 cm2
      3. Notice that the ones place now varies and we really have no idea what the tenths or hundredths place would be, so we should round this answer to the ones place.
      4. Using our original measurements we get: 12 cm x 1.33 cm = 15.96 cm2 --- rounded to ---> 16 cm2
    4. Try some practice problems for doing calculations significant digits.

 

 

 

 

 

 

 

 

 

 

 

 

The numbers which are in bold are definitely significant. The green numbers may or may not be significant depending on how the measurement was made.

3.456 -> 4
5.000 -> 4
10003 -> 5
0.666 -> 3
5.001 -> 4
0.00300 -> 3
5 -> 1
0.005 -> 1
314.000 ->6
10000 -> 1 to 5
12000 -> 2 to 5
10000.0 -> 6
100321 -> 6
90210 -> 4 to 5
314000 -> 3 to 6